Autoria do Prof. Rodolpho Caniato
Desde a antiguidade sabe-se e percebeu-se que as marés mais altas e também as mais baixas, ocorrem tanto na lua cheia quanto na lua nova. Essas marés são chamadas de marés de sizígia. Esta palavra, usada até hoje pelas marinhas, já era usada pelos gregos e mais tarde pelos romanos, antes da nossa era. Sizígia que dizer conjunção ou alinhamento. Tanto na lua cheia quanto na nova, Terra, Sol e Lua estão em conjunção, isto é, aproximadamente alinhados. Quando se olha para a lua cheia, toda branca, redonda e iluminada, no horizonte, tem-se o Sol exatamente na sua nuca. Quando é lua nova, nosso satélite natural fica bem na direção do Sol e, por isso, ofuscado pelo brilho desse, a menos que passe bem na frente dele. Neste caso teremos, além de lua nova, um eclipse do Sol. Do ponto de vista da Física, com linguagem matemática, é simples a explicação para o fenômeno das marés. Aqui, no entanto, espero fazer com que o leitor possa entender este fato curioso e importante, usando a experiência que temos de nossas vidas diárias, sem o uso de fórmulas matemáticas ou físicas.
Se não existissem a Lua e o Sol, não haveria o efeito das marés. As águas ao redor da Terra teriam sempre uma distribuição esférica. O nível do mar permaneceria sempre o mesmo. Comecemos por tratar de entender o efeito da presença da Lua como a maior causa para as marés. Você já deve ter visto ou sabido de uma brincadeira de crianças que se chama corrupio. Em meu tempo de infância, no Rio de Janeiro, essa brincadeira era comum entre pares de meninas. A brincadeira consiste em um par rodopiar de mãos dadas. À medida que as meninas rodopiam, uma ao redor da outra, as mãos dadas seguram para que elas não se separem. Se ambas têm o mesmo peso (a rigor, mesma massa), as duas farão voltas iguais, ao redor do centro (de massa) do par, exatamente na metade da distância que separa as duas. Imaginemos agora que uma delas é bem mais pesada que a outra. Agora, a menor fará voltas maiores e a maior fará voltas menores, mas no mesmo tempo. Se uma delas for muito mais pesada, elas continuarão a fazer suas voltas em tempos iguais. Também as forças com que cada uma puxa a outra são iguais. No entanto, aquela que é muito mais pesada fará um movimento muito menor, enquanto a mais leve fará uma volta muito maior. A maior fará também voltas, só que ao redor do centro de massa que agora está muito mais perto dela. Pode até esse centro estar tão próximo dela, da mais gorda, quero dizer da mais pesada, que seu movimento vai se reduzir a uma espécie de “rebolado” ou bamboleio.
Essa brincadeira imaginária servirá para ajudá-lo a entender o fenômeno das marés. As meninas brincando de corrupio representam a Terra e a Lua. As duas têm pesos (massas) muito diferentes. No caso, a Terra, em termos de massa, equivale a aproximadamente 80 vezes a Lua. Isso significa que seriam necessárias 80 Luas para equilibrar uma Terra, se puséssemos as duas em uma imaginária balança de pratos iguais. As meninas brincando de corrupio se mantinham unidas pela força que ambas fazem mutuamente unidas. A Terra e a Lua se mantêm unidas pelos “braços” invisíveis da mútua atração gravitacional. O fato de a Terra ter massa muitas vezes maior que a da Lua faz com que seu movimento seja muito menor, como a menina mais pesada no corrupio. Enquanto a Lua faz uma volta muito maior, a Terra faz apenas uma espécie de “rebolado” ou bamboleio ao redor do centro de massa das duas. Isso porque o centro de massa do sistema Terra-Lua está dentro da Terra, mais próximo à superfície.
Agora imagine que a “menina maior”, muito gorda, redonda, tem um “vestido”, o mar, que lhe envolve todo o corpo e dentro do qual ela pode se mover livremente. A menina menorzinha não está envolvida por nenhuma roupa (mar ou atmosfera). A atração entre as duas não tem nada para deformar na menina menor, mas tem na maior. O “vestido da maior”, do lado da menor será puxado para ela, isto é, fica com uma saliência voltada para a menor. Do lado oposto seu “vestido” fará também uma saliência, devida ao seu “rebolado” ou bamboleio. Em resumo: a menina menor não tem nenhum vestido para ser deformado. A maior, no entanto, tem um vestido que envolve todo seu corpo “gordo” e redondo. Esse “vestido” deformável, dentro do qual ela se move apresentará duas saliências iguais e opostas: uma voltada para a “menina” menor e outra em direção contrária ou “para trás”.
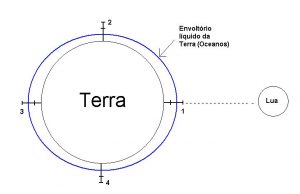
Entendido o corrupio das duas meninas, fica mais fácil entender o fenômeno das marés. A menorzinha das meninas, a Lua, não tem qualquer “vestido” que possa ser deformado na direção da “gorda”, a Terra. Esta, sim, é envolvida por um “vestido”, o mar que lhe cobre quase três quartas partes do “corpo” bem redondo. Se não houvesse essa “brincadeira”, o “vestido” da Terra, a água que lhe cobre quase todo o corpo teria uma distribuição esférica. A atração mútua em rodopio deforma a distribuição esférica do “vestido” de água da Terra. Com isso a distribuição das águas ao redor da Terra, em vez de esférica, assume uma forma de elipsoide cujo eixo mais longo fica na direção Terra-Lua (veja a figura no início do texto). Elipsoide é uma forma que lembra uma “bola” de futebol americano.
Nota: leia também: (links)
A IMPORTÂNCIA DAS MARÉS (I)
A LUA EXERCE EFEITO SOBRE OS SERES VIVOS? (III)